Adsorption of acetic acid on charcoal and the isotherm

Adsorption of acetic acid on charcoal and validity of Freundlich’s adsorption isotherm and Langmuir’s adsorption isotherm

Adsorption of acetic acid on charcoal is the topic of discus for today. Adhesion to a surface is called the adsorption of atoms, ions, biomolecules, or gas, liquid, or dissolved solids molecules. The activated charcoal adsorbs acetic acid. The activated charcoal adsorbs the acids in their porous meanwhile this process follows the adsorption isotherm of Freundlich as well as isotherm of Langmuir. Adsorption of acetic acid on activated charcoal is a very important topic to understand the validity of Freundlich’s adsorption isotherm as well as Langmuir’s adsorption isotherm.

The amount adsorbed by an adsorbent is dependent on pressure and temperature. Thus the amount (X) adsorbed is a function of pressure (P) and temperature (T), i.e.

X= f(P,T)

A plot of P vs X, keeping temperature constant is known as adsorption isotherm.

Freundlich’s adsorption isotherm:

Freundlich’s adsorption isotherm; represented by –

X/m = kc^1/n

where m= the amount of adsorbing material C is the equilibrium constant of adsorbate in the solution k is the constant depending on the nature of both adsorbate and adsorbant n is another constant depending on the nature of both adsorbates.

The value of 1/n is less than unity. On taking the logarithm of the equation,

log (x/m)= 1/n log c + log k         —————————— (2)

If a plot of log (x/m) vs log c gives a straight line with a slope of 1/n and intercept of log k, Freundlich’s adsorption isotherm is valid

Langmuir’s adsorption isotherm:

According to Langmuir for a uni-molecular layer, the following relation holds for adsorption,

x/m = k₁k₂c/(1+k₁c)

where k₁ and k₂ are the constant.

The above equation can be written as-

c/(x/m) = 1/ k₁k₂ + c/k₂

Thus a plot of c/(x/m) vs c gives a straight line with a slope of 1/k₂ and an intercept of 1/ k₁k₂ and shows the validity of Langmuir adsorption isotherm

Apparatus and chemicals:

Burette, pipette, Activated charcoal, 0.5N acetic acid, 0.1N NaOH, Stopped bottles, Shaking machine, etc.

Procedure:

• Prepare 0.5N acetic acid as well as 0.1N NaOH solution.
• Take 6 clean and dry stopped bottles and prepare the following solutions in the table-

Bottle No	0.5N Acetic acid(mL)	Distilled water (mL)	Amount of charcoal (g)
01.	50	0	1
02.	40	10	1
03.	30	20	1
04.	25	25	1
05.	20	30	1
06.	10	40	1

• Spotted each bottle after that shake for at least 1 hour.
• Filter the solution through filter paper as well as collect the filtrate in the numbered bottle. reject the first 5 mL of each filtrate.
• Pipette out 10 mL of each filtrate and titrate with 0.1N NaOH solution.
• Note Down the temperature of the solution.

Data :

Bottle No: 01

Activated solution (mL)	IBR	FBR	BR difference	mean
10	0	a1	a1	let the mean be x1
10	a1	b1	a1-b1
10	b1	c1	b1-c1

Bottle No: 02

Activated solution (mL)	IBR	FBR	BR difference	mean
10	0	a2	a2	let the mean be x2
10	a2	b2	a2-b2
10	b2	c2	b2-c2

Bottle No: 03

Activated solution (mL)	IBR	FBR	BR difference	mean
10	0	a3	a3	let the mean be x3
10	a3	b3	a3-b3
10	b3	c3	b3-c3

Bottle No: 04

Activated solution (mL)	IBR	FBR	BR difference	mean
10	0	a4	a4	let the mean be x4
10	a4	b4	a4-b4
10	b4	c4	b4-c4

Bottle No: 05

Activated solution (mL)	IBR	FBR	BR difference	mean
10	0	a5	a5	let the mean be x5
10	a5	b5	a5-b5
10	b5	c5	b5-c5

Bottle No: 06

ActivatedActivaated solution (mL)	IBR	FBR	BR difference	mean
10	0	a6	a6	let the mean be x6
10	a6	b6	a6-b6
10	b6	c6	b6-c6

Calculation:

Bottle No	Initial conc. of the acetic acid before adsorption (C0)	Equilibrium conc. of the acetic acid before adsorption (Ce)	Amount of acetic acid adsorped (C0-Ce)
01	50	x1	y1
02	40	x2	y2
03	30	x3	y3
04	25	x4	y4
05	20	x5	y5
06	10	x6	y6

Table for the proof of Freundlich’s adsorption isotherm

Bottle No.	Amount of acetic acid adsorped (C0-Ce) = (x/m)	log(x/m)	Ce= C	log C
01	y1	log y1	x1	log x1
02	y2	log y2	x2	log x2
03	y3	log y3	x3	log x3
04	y4	log y4	x4	log x4
05	y5	log y5	x5	log x5
06	y6	log y6	x6	log x6

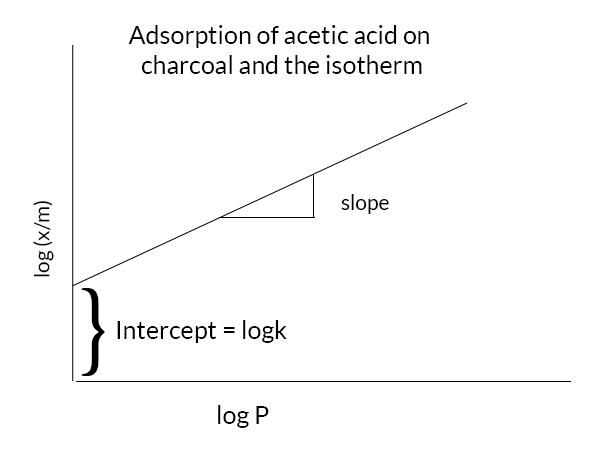
Freundlich’s adsorption equation

log(x/m) = logk +1/n logC

from the above graph, we can see that the graph is a straight line and the slope is 1/n the intercept is log k. we can find the value of k from the intercept.

Table for the plot of Langmuir adsorption isotherm:

Bottle No.	Equilibrium conc. of the acetic acid before adsorption (Ce)	Amount of acetic acid adsorped (C0-Ce) = (x/m)	Ce /(x/m)
01	x1	y1	x1/y1
02	x2	y2	x2/y2
03	x3	y3	x3/y3
04	x4	y4	x4/y4
05	x5	y5	x5/y5
06	x6	y6	x6/y6

From the Langmuir equation

Ce/(x/m) = 1/(k₁k₂) + c/k₂

from the above graph, we can see that the graph is a straight line and the slope is 1/k₂ the intercept is 1/(k₁k₂). we can find the value of k₂ from the slop. After that, we can also find the k₁ from the intercept and the value of k₂.

The concentration of acetic acid after adsorption:

1. The initial concentration of acetic acid is = 0.50N
2. Calculation of the equilibrium concentration of acetic acid:

we know, VaSa = VbSb Sa=VbSb/Va

here, Va= Volume of Acetic acid Vb= Volume of NaOH Sa= Concentration of Acetic acid Sb=Concentration of NaOH

Bottle No.	Sa
01	S1
02	S2
03	S3
04	S4
05	S5
06	S6

Result:

1. The validity of Freundlich’s adsorption isotherm is proved from the above first plot. 
2. The validity of the Langmuir adsorption isotherm is proved from the above second plot. 

Follow Us On Facebook, Twitter, Linkedin, and Tumbler.

Read more

KMnO4 + H2SO4 + Na2SO3 = K2SO4 + MnSO4 + Na2SO4 + H2O

Balancing K2Cr2O7 + FeCl2 + HCl = KCl + CrCl3 + FeCl3 + H2O

Chemical reaction-Types of chemical reactions